Consensus Protocol Using TLA+

Looking to dive into distributed systems research, I recently started learning how to write TLA+ specifications. TLA+ is a specification language used to mathematically describe an algorithm, and is adopted in both academia and industry. It provides functionalities to formally verify algorithm correctness. Precisely, it allows us to check if an algorithm satisfies the properties we want it to satisfy.

In this post I shall discuss a TLA+ specification of Consensus I wrote. This specification describes the properties of Consensus at its highest level. That is, we are not concerned with how a specific protocol can achieve Consensus, but what properties should any solution to Consensus possess. It is thus useful for now to forget about mechanisms such as message-passing; a system that solves Consensus using extrasensory perception solves it equivalently as one using TCP.

Consensus

The Consensus problem is easy to state and understand. Yet it is the basic building-block of computer systems requiring coordination between agents.

Fundamentally, a protocol that solves Consensus in a synchronous system permitting crash failures must have the following properties.

1. Validity: If all processes that propose a value propose \(v\), then all correct processes eventually decide \(v\).
2. Agreement: If a correct process decides \(v\), then all correct processes eventually decide \(v\).
3. Integrity: If a correct process decides \(v\), then some process must have proposed \(v\).
4. Termination: Every correct process eventually decides some value.

Agreement and Integrity are safety properties: they dictate that inconsistent decisions cannot occur. Validity and Termination are liveness properties: they prevent processes from trivially deciding, say, 0 in all cases, and from not halting.

For our present purpose let us consider, without loss of generality, Binary Consensus, in which each participant proposes either 0 or 1.

TLA+ Model

State Machines and Mathematical Functions

To model Consensus mathematically as in TLA+, we adopt a state machine approach. Each participant in the protocol undergoes the following state transitions:

All processes begin in the working state. They then each propose a value, either 0 or 1, to the system. After which, all correct processes then deterministically decides on one of the proposed values (we do not yet care how).

To express these state transitions as math, we begin by defining some constants and variables. In TLA+, we write

CONSTANTS PCS  \* The set of all processes

VARIABLES   states,     \* states of each process in PCS
            proposals,  \* proposals of each process in PCS
            pset,       \* set of all proposals 
            decisions   \* decision of each process in PCS

\(PCS\) and \(pset\) are mathematical sets. It may be intuitive at first to think of the variables \(states\), \(proposals\) and \(decisions\) as arrays in a programming language, mapping each process id to its respective state, proposal and decision. However, such intuition is not correct. TLA+ does not operate in the realm of memory addresses. The language of TLA+ is mathematics, and in math, arrays are functions with domain \(\mathbb{N}\) (the natural numbers).

But unlike arrays, TLA+ functions do not restrict us to any particular domain. Here, I shall define \(states\), \(proposals\) and \(decisions\) as functions mapping \(PCS\), the set of all processes, to their respective state, proposal and decision values.

Init

At the heart of all state machines, and indeed any TLA+ spec, are statements describing the initial state of the system, and how it transitions from one state to the next. In my model, while each process is a state machine, the entire system as a whole is itself a state machine, and it is this global state machine we describe in TLA+. Therefore, we can think of the behavior Consensus, and indeed any system, as a sequence of state transitions

\[S_0 \rightarrow S_1 \rightarrow S_2 \rightarrow S_3 \rightarrow ...\]

In TLA+, we define \(init\) as a boolean formula describing the properties of the initial state \(S_0\). I describe the initial state of the Consensus as so:

init == /\ states = [p \in PCS |-> "working"]
        /\ proposals \in [PCS -> {0, 1}]
        /\ pset = {}
        /\ decisions = [p \in PCS |-> -1]

This is a logical conjunct of four statements

1. \(states\) is the function \(states : PCS \rightarrow \{``working", ``proposed", ``decided"\}\) such that \(\forall p \in PCS : states(p) \mapsto ``working"\).
2. \(proposals\) is some function \(proposals : PCS \rightarrow \{0, 1\}\). TLA+ will then iterate through all such functions.
3. \(pset\) is the empty set.
4. \(decisions\) is the function \(decisions : PCS \rightarrow \{-1, 0, 1\}\) such that \(\forall p \in PCS : decisions(p) \mapsto -1\), with \(-1\) as the placeholder for not having yet decided.

Note that in each statement, we are not performing variable assignments. Instead, statements 1 through 4 are boolean statements. For instance, statement 1 asserts that \(states\) is indeed the function described. And thus, the statement we call \(init\) is a boolean statement asserting the properties of the initial state of Consensus – any system at its initial state \(S_0\) satisfies the initial spec of Consensus if and only if \(init\) is true when applied to \(S_0\).

Next

While \(init\) asserts what must be true in \(S_0\), the \(next\) formula describes the state transition

\[S_i \rightarrow S_{i+1}\]

Thus intuitively, if \(init\) is the base case for an inductive proof, then \(next\) is the inductive step. If \(init\) is true on \(S_0\), and \(next\) is true on \(S_i \rightarrow S_{i+1}\) for all \(i = 0, 1, 2, 3...\), then our system behaves correctly as specified.

For my Consensus spec, I split \(next\) into two possible actions of the system – any process can either choose to propose a value (if it has not yet done so), or decide a value (after all processes have proposed). I write \(propose\) as so:

propose(p) == /\ states[p] = "working"
              /\ states' = [states EXCEPT ![p] = "proposed"]
              /\ pset' = pset \cup {proposals[p]}
              /\ UNCHANGED <<proposals, decisions>>

Again, it is the logical conjunct of four statements that say that in a transition \(S_i \rightarrow S_{i+1}\) where process \(p\) proposes a value:

1. In \(S_i\), \(states(p) \mapsto ``working"\), i.e. \(p\) has not yet proposed.
2. In \(S_{i+1}\), \(\forall q \ne p : states_{S_{i+1}}(q) \mapsto states_{S_i}(q)\) and \(states_{S_{i+1}}(p) \mapsto ``proposed"\), i.e. all states are unchanged except that of \(p\).
3. In \(S_{i+1}\), \(pset\) now contains the value \(proposal(p)\).
4. In \(S_{i+1}\), the functions \(proposals\) and \(decisions\) are exactly those in \(S_i\).

Likewise, I express \(decide\) as:

decide(p) == /\ ~ \E r \in PCS : states[r] = "working"
             /\ states[p] = "proposed"
             /\ states' = [states EXCEPT ![p] = "decided"]
             /\ decisions[p] = -1
             /\ decisions' = [decisions EXCEPT ![p] = CHOOSE x \in pset : TRUE]
             /\ UNCHANGED <<proposals, pset>>

It describes the transition where process \(p\) proposes a value, and is the logical conjunct of:

1. In \(S_i\), there does not exist any process \(q\) such that \(states(q) \mapsto ``working"\), i.e. every process has proposed.
2. In \(S_{i+1}\), \(\forall q \ne p : states_{S_{i+1}}(q) \mapsto states_{S_i}(q)\) and \(states_{S_{i+1}}(p) \mapsto ``decided"\), i.e. all states are unchanged except that of \(p\).
3. 1. In \(S_i\), \(decisions(p) \mapsto -1\), i.e. \(p\) has not yet decided.
4. In \(S_{i+1}\), \(\forall q \ne p : decisions_{S_{i+1}}(q) \mapsto decisions_{S_i}(q)\) and \(decisions_{S_{i+1}}(p)\) maps to some deterministically chosen value from \(pset\). In the semantics of TLA+, this value will be the same for all processes.
5. In \(S_{i+1}\), the functions \(proposals\) and \(decisions\) are exactly those in \(S_i\).

Finally, we can express \(next\) as simply

\[next \equiv \exists p \in PCS : propose(p) \lor decide(p)\]

which means that in any step \(S_i \rightarrow S_{i+1}\) there exists a process \(p\) which either proposes or decides a value. When such a process does not exist, then the protocol halts. In TLA+ syntax, that’s

next == \E p \in PCS : propose(p) \/ decide(p)

Checking for Correctness

The protocol is complete. Now we want to make sure that if \(init\) and \(next\) are true on

\[S_0 \rightarrow S_1 \rightarrow S_2 \rightarrow S_3 \rightarrow ...\]

, then we satisfy the spec of Consensus that is validity, agreement, integrity and termination. TLA+ allows us to do exactly that by expressing these as invariants.

But first, we also want to make sure we did not break any type requirements by specifying the invariant \(typeOK\). I shall omit detailed descriptions as the syntax is similar to what I have described above.

typeOK == /\ states \in [PCS -> {"working", "proposed", "decided"}]
          /\ proposals \in [PCS -> {0, 1}]
          /\ pset \subseteq {0, 1}
          /\ decisions \in [PCS -> {-1, 0, 1}]

Finally, we have the invariants

validity == \E v \in {0, 1} : (\A p \in PCS : proposals[p] = v) 
                => \A q \in PCS : (states[q] = "decided" 
                    => decisions[q] = v)

agreement == \A p1, p2 \in PCS : ~ /\ decisions[p1] = 0
                                   /\ decisions[p2] = 1
                                  
integrity == \A p \in PCS : 
                (states[p] = "decided" 
                => \E r \in PCS : proposals[r] = decisions[p])

specOK == /\ validity
          /\ agreement
          /\ integrity

Here, the only syntax we have yet seen is =>, which represents logical implication. Therefore, the menacing description for \(validity\) means, quite simply, that, if there exists a value \(v \in \{0, 1\}\) such that everyone proposed \(v\), then at any time for all processes \(q\), if \(q\) has decided, then \(q\) must have decided \(v\).

But what about termination? Well, termination means that the protocol halts. In TLA+, that is characterized as a form of deadlock, and TLA+ has built-in detection for that.

We then set up a TLA+ model as so, telling it to check the behavior described by \(init\) and \(next\) against the invariants, and for deadlock.

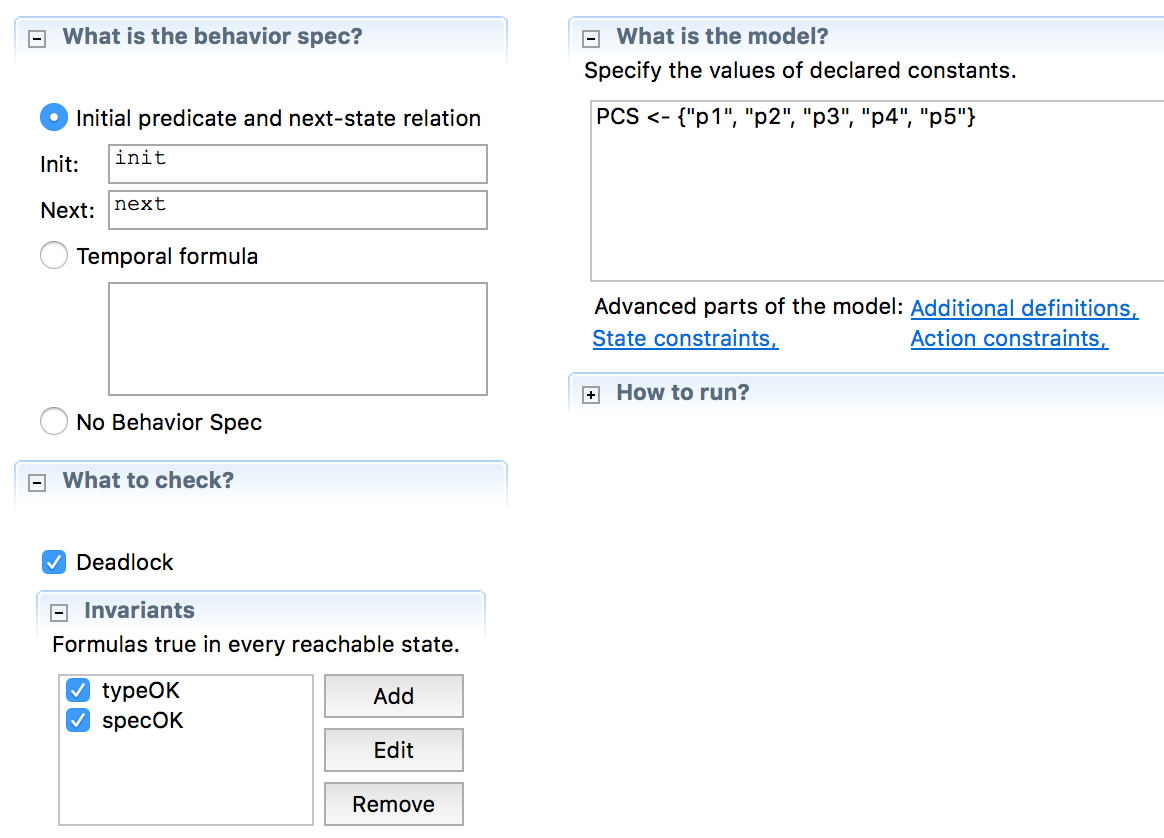
Running the model tells us what we have is correct.

Concluding Remarks

It does seem that the Consensus protocol I have described works like magic. There is no message passing, and processes spontaneously decide on a value from a global set. Yet this is the goal. As emphasized above, this is a high-level description of what Consensus should do, and not how it achieves it.

Of course, TLA+ also allows us to specify a particular implementation of Consensus, complete with message passing and the like. But the point of having done as we did here is that using TLA+, we can later check any specific implementation against this high-level specification we have written. In other words, a specific instance of Consensus is correct if it implies that the general spec is satisfied. I will explore doing that in later post.

Lastly, TLA+ lets us pretty-print our spec, so it looks nicely formatted in latex-style math. You can check out the pretty-printed version of this spec, and the code itself, on my GitHub page.